2017学年第一学期位育中学监控考试
高中三年级数学
填空题
1.若集合
，集合
，且，则
的取值范围为______.
2.若虚数
是实系数方程
的一个根，则
的值为_______.
3.函数
的概念域是______.
4. 
=_______.
5.假如矩阵
是线性方程
的增广矩阵，则这个线性方程的解
可用矩阵表示为_______.
6.已知指数函数
在概念域内为减函数，则实数的取值范围______.
7.已知等比数列
的公比为
，前
项和为，且
成等差数列，则
的值为______.
8.某电视台连续播放5个广告，其中3个不一样的商业广告2个不一样的奥运宣传广告，则最后播放的是奥运宣传广告，且2个奥运宣传广告不连续播放的概率是______.
9. 
的展开式中各项系数和为2，则展开式中常数项为______.
10.若
是椭圆
的左、右两个焦点，
是椭圆上的动点，则
的最小值为________.
11.若数列的通项公式是
，则
等于______.
12.在平行四边形中，
是线段
上一点，且满足，若
为平行四边形内任意一点（含边界），则
的最大值为______.
2、选择题
13.在所对的边分别为，则
的值等于（ ）
A．
B． C．
D．
14.若点
是棱长为1的正方体
中异于的一个顶点，则
的所大概值的个数是（ ）
A．1 B．2 C．3 D．4
15.若直线与曲线
交于不一样的两点，则
的取值范围是（ ）
A. B. C. 
D.
16.设是二次函数，若
的值域是
，则
的值域是（ ）
A. B. C. D.
3、解答卷
17.如图，在四棱锥中，底面是矩形，
底面，
的中点，已知
，求：
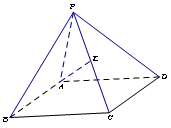（1）三角形的面积；
（2）异面直线所成角的大小；
18．在在所对的边分别为
，
（1）求的值；
（2）若求向量方向上 的投影。
19.已知函数
（1）若求的取值范围；
（2）若是以2为周期的偶函数，且，求函数
的反函数。
20.已知数列，
（1）设是公差为3的等差数列，当的值；
（2）设，求正整数,使得对所有均有
（3）设
时，求数列
的通项公式。
21.已知椭圆方程为，长轴两端点为
，短轴的上端点为
（1）若椭圆焦点坐标为，点在椭圆上运动，当
的最大面积为3时，求其椭圆方程；
（2）对于（1）的椭圆方程，作以为直角顶点的内接于椭圆的等腰
，设直线的斜率为，试求满足的关系式：
（3）过任作在椭圆上，试问在轴上是不是存在一点
使得直线
的斜率与的斜率之积为定值，假如存在，找出点的坐标和定值，假如没有，说明理由。
